Matt Mahoney
Updated Feb. 23, 2004
One limitation of this approach is that rule induction finds only the minimal set of rules to distinguish segments. For anomaly detection, tighter rules are desired. To illustrate, consider the following example of a trace with two segments:
Training: __/ Segment 1: x = 0, dx = 0, ddx = 0
Segment 2: 0 < x < 1, dx = 1, ddx = 0
Test: __| Segment 1: x = 0, dx = 0, ddx = 0
Segment 2: 0 < x < 1, dx = 10, ddx = 0
The quantities dx and ddx are the first and second derivatives of x,
respectively. A rule induction algorithm would find the simplest set
of rules that distinguishes the two segments, i.e.
if dx > 0.5 then segment 2 else segment 1These rules are then used to construct the following state machine:
+---+ dx > 0.5 +---+
Start --->| 1 |------------->| 2 |----> Accept
+---+ +---+
This machine would accept the test trace, even though a direct comparision
of the the points in test segment 2 do not match any points anywhere
in the training trace.
dx
^
|
|
10 oooo o = test trace
. o
. o x = training trace
. o
2 o
o
1 xxxx
x
0 x--------------> x
0 1 2 3 4
Both start at x = 0, dx = 0 and remain there throughout
segment 1. The training trace, marked
with "x", then jumps to (0,1) and moves right to (1,1) during segment 2.
On the other hand, the test trace jumps to (0,10), then moves right to
(1,10). During this time, its distance to the nearest point in the
training trace is 9. We define the square of this distance (81) to
be the error, which we assign to all of the points in test segment 2.
In this example, the path traced by the training data fits a unit square. We always scale the dimensions so that the training data spans a unit cube so that the error is independent of the units used in the time series.
Because the data may be noisy, it is passed through two low-pass filters after each sampling or differentiation step. Experimentally, a time constant of T = 5 samples for each filter works well. The path dimensions x, dx, and ddx are computed as shown:
x dx ddx
sample --> LP --> LP ---> D --> LP --> LP ----> D --> LP --> LP ---->
where:
x y
---> LP ---> means y(t) = (1 - 1/T)y(t-1) + x(t)/T (low pass filtering step)
x y
---> D ---> means y(t) = x(t) - x(t-1) (differentiation step)
and x(t) and x(t-1) mean the current and previous values of x, respectively.
A model is trained by storing all (x,dx,ddx) points in the training trace. A test point P (px,pdx,pddx) is assigned an error equal to the square of the Euclidian distance to the nearest training point Q = (qx,qdx,qddx),
Error = min[((px - qx)/(max x - min x))2
+ ((pdx - qdx)/(max dx - min dx))2
+ ((pddx - qddx)/(max ddx - min ddx))2]
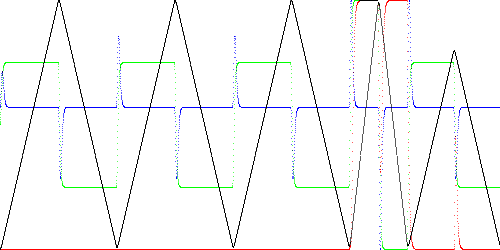
Figure 1 below illustrates the process. The time series (x) is a triangle
wave (black line) with 1000 samples per cycle. The green and blue lines
are the filtered first and second derivatives (dx and ddx) respectively.
The model is trained on the first two cycles. The error (shown filtered with
a time constant of 10 samples for visibility) is red. The first
two cycles are training, so the error is 0. The third cycle is identical,
so there is no error here either.
The fourth cycle is too steep, which increases the
amplitude of the first derivative. This causes a large error during the
rise and fall portions of the waveform. (A state machine model would
miss this). The fifth waveform has the correct slope, but is too short,
resulting in an error spike at the peak. The error is due to the
absence of the simultaneous occurrence of the observed values of
x (black) and ddx (blue) in the training data.

Fig. 1. Example of a time series (black), its first derivative (green), second derivative (blue), and anomaly score (red).
x1 x2 x3
sample ---> LP1 ---> LP2 ---> LP3 ---> LP4 --->
The four low pass filters have increasingly long time constancts, for
example T = 5, 5, 20, and 100 samples for LP1 through LP4 respectively.
The signals x2 and x3 represent a delayed average of x1 over
a time window of approximately T (with an exponential decay). Thus,
these signals represent state information.
Figure 2 shows the effect of filter modeling the previous data. The signals x1, x2, and x3 are shown in black, green, and blue respectively. Once again, the model is trained on the first two waveforms. The red line shows the anomaly score.
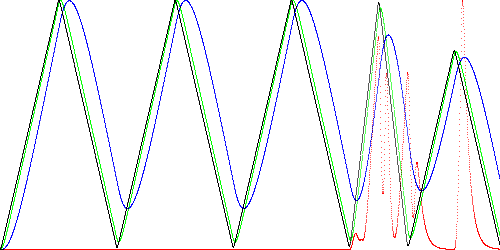
Fig. 2. Example time series (black), two filtered versions (green and blue), and anomaly score (red).
In the following experiments, we evaluate a test trace by the maximum error for any test point, and by the total error over all test points. We use 3 models for each data set:
Table 1. TEK anomaly scores
Derivative Max error Total error ------------ --------- ----------- TEK00000.CSV (training) 0.000000 0.000000 TEK00001.CSV (test, normal) 0.001083 0.146480 TEK00002.CSV (test, abnormal...) 0.004820 0.574574 (lowest error) TEK00003.CSV 0.004899 0.662828 TEK00010.CSV 0.022418 0.488846 TEK00011.CSV 0.007575 1.486843 TEK00012.CSV 0.010881 0.480255 TEK00013.CSV 0.029057 3.556351 TEK00014.CSV 0.029646 7.420616 TEK00015.CSV 0.029283 5.787726 TEK00016.CSV 0.043123 6.459918 TEK00017.CSV 0.029842 3.773003 Filter, short delay Max error Total error ------------ --------- ----------- TEK00000.CSV 0.000000 0.000000 TEK00001.CSV 0.002272 0.379665 TEK00002.CSV 0.008385 1.516945 (lowest error) TEK00003.CSV 0.008854 1.775839 TEK00010.CSV 0.156160 4.246407 TEK00011.CSV 0.057814 5.098161 TEK00012.CSV 0.101912 2.835300 TEK00013.CSV 0.082527 9.736537 TEK00014.CSV 0.082630 21.864046 TEK00015.CSV 0.082068 16.784515 TEK00016.CSV 0.265216 20.980508 TEK00017.CSV 0.087048 10.243923 Filter, long delay Max error Total error ------------ --------- ----------- TEK00000.CSV 0.000000 0.000000 TEK00001.CSV 0.011262 0.869624 TEK00002.CSV 0.033206 2.827358 (lowest error) TEK00003.CSV 0.046835 4.265036 TEK00010.CSV 0.119588 9.066618 TEK00011.CSV 0.050149 6.671413 TEK00012.CSV 0.083966 8.519004 TEK00013.CSV 0.060676 11.009125 TEK00014.CSV 0.196175 31.669394 TEK00015.CSV 0.115931 17.818679 TEK00016.CSV 0.524050 27.891036 TEK00017.CSV 0.058432 7.434122
Fig. 3. shows the anomaly score (in red) for the 5 traces TEK-0 (training), TEK-1 (normal), and TEK-10, TEK-11, TEK-12 (abnormal) using derivative modeling. Note that TEK-10 and TEK-12 lack a spike on the rising and falling edges of the main waveform, indicating that the poppet failed to move when energized. The error is greatest in these regions. Fig. 4 shows similar results for filter modeling with short delay.

Fig. 3. Derivative path anomaly score (red) for TEK-0, 1, 10, 11, 12.
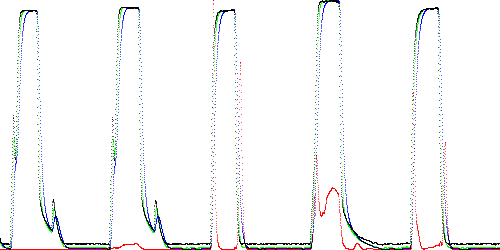
Fig. 4. Short delay filter path anomaly score (red). The first two filter stages are shown in green and blue.
Table 2. Voltage Test 1 Anomaly Scores.
Derivative Max error Total error ----------------------- --------- ----------- V37898 V32 T21 R00s.txt 0.000000 0.000000 (train) V37898 V32 T21 R01s.txt 0.000314 0.004077 (normal) V37898 V32 T22 R02s.txt 0.000182 0.007974 (normal) V37898 V32 T70 R03s.txt 0.006866 4.212239 (hot) V37898 V32 T22 imp045 R01s.txt 0.006276 0.070143 (4.5 mil blockage) V37898 V32 T22 imp09 R01s.txt 0.006313 0.095901 (9 mil blockage) V37898 V30 T21 R00s.txt 0.002611 0.214189 (30 volts) Filter, short delay Max error Total error ----------------------- --------- ----------- V37898 V32 T21 R00s.txt 0.000000 0.000000 (train) V37898 V32 T21 R01s.txt 0.000506 0.009210 (normal) V37898 V32 T22 R02s.txt 0.000581 0.023369 (normal) V37898 V32 T70 R03s.txt 0.118664 36.191784 (hot) V37898 V32 T22 imp045 R01s.txt 0.001601 0.057184 (4.5 mil blockage) V37898 V32 T22 imp09 R01s.txt 0.002322 0.074015 (9 mil blickage) V37898 V30 T21 R00s.txt 0.009154 2.943229 (30 volts) Filter, long delay Max error Total error ----------------------- --------- ----------- V37898 V32 T21 R00s.txt 0.000000 0.000000 (train) V37898 V32 T21 R01s.txt 0.000534 0.051832 (normal) V37898 V32 T22 R02s.txt 0.000553 0.067666 (normal) V37898 V32 T70 R03s.txt 0.144647 48.025722 (hot) V37898 V32 T22 imp045 R01s.txt 0.001361 0.088319 (4.5 mil blockage) V37898 V32 T22 imp09 R01s.txt 0.001769 0.097798 (9 mil blockage) V37898 V30 T21 R00s.txt 0.009671 3.439430 (30 volts)

Fig. 5. Derivative path anomaly scores (red) for the training trace (left), 9 mil blockage (center), and 30 volts (right).
Once again, the normal traces have lower maximum and total error scores in every case by a factor of at least 8 for derivative modeling. The margins for filter modeling are smaller, especially for detecting blockage with long filter delays. In all cases, voltage and temperature anomalies occur mainly over the steady "on" phase due to lower solenoid current. The plunger blockage anomalies occur mainly on the rising and falling edges due to the reduced height of the smaller spikes on these edges (barely visible in Fig. 5).
The third test simulates (using LabView) two batteies charging and discharging in cycles, generating an approximate sawtooth waveform with Gaussian noise added. Each trace has about 1000 samples. The first 10 are normal operation with various amounts of noise added. The second 10 simulate over or under voltage on one or both batteries, with or without noise.
In this test, only battery 1 voltage was monitored. All 10 of the normal traces were used for training. The traces with faults on battery 2 only are thus considered normal. All of these (runs 12, 15, 17, and 20) have lower total and maximum anomaly scores than the corresponding faults on battery 1. Unlike the previous results, the margin for noisy low voltage detection (the hardest condition to detect) is greater using filter path modeling than derivative path modeling.
Table 3. Simulated battery charger anomaly scores.
Derivative model Max error Total error
--------------------- --------- -----------
run01_norm_noise0.txt 0.000000 0.000000
run02_norm_noise0.txt 0.000000 0.000000
run03_norm_noise0.txt 0.000000 0.000000
run04_norm_noise0.txt 0.000000 0.000000
run05_norm_noise0.txt 0.000000 0.000000
run06_norm_noise125.txt 0.000000 0.000000
run07_norm_noise250.txt 0.000000 0.000000
run08_norm_noise500.txt 0.000000 0.000000
run09_norm_noise1000.txt 0.000000 0.000000
run10_norm_noise2000.txt 0.000000 0.000000
run11_high1_noise0.txt 31.437864 30677.092300 (test starts)
run12_high2_noise0.txt 27.108379 116.008183 (normal)
run13_high12_noise0.txt 31.437859 28908.636333
run14_low1_noise0.txt 27.108379 113.293984
run15_low2_noise0.txt 0.011733 0.152721 (normal)
run16_high1_noise500.txt 18.968859 1895.435037
run17_high2_noise500.txt 4.952080 18.280882 (normal)
run18_high12_noise500.txt 16.724800 1711.298450
run19_low1_noise500.txt 0.453953 4.695456
run20_low2_noise500.txt 0.032621 2.585849 (normal)
Filter, short delay (test only) Max error Total error
--------------------- --------- -----------
run11_high1_noise0.txt 145.031738 138531.347230
run12_high2_noise0.txt 139.909599 1832.311864 (normal)
run13_high12_noise0.txt 145.031738 130538.508992
run14_low1_noise0.txt 139.909599 1868.606235
run15_low2_noise0.txt 0.072515 1.735517 (normal)
run16_high1_noise500.txt 38.771435 9961.071482
run17_high2_noise500.txt 13.703833 193.563394 (normal)
run18_high12_noise500.txt 33.249472 9137.153585
run19_low1_noise500.txt 8.897319 137.127072
run20_low2_noise500.txt 0.542675 17.138300 (normal)
Filter, long delay (test only) Max error Total error
--------------------- --------- -----------
run11_high1_noise0.txt 173.115294 153079.154788
run12_high2_noise0.txt 168.281784 6275.809724 (normal)
run13_high12_noise0.txt 173.108290 144228.611260
run14_low1_noise0.txt 168.274850 6089.356835
run15_low2_noise0.txt 0.192869 11.164502 (normal)
run16_high1_noise500.txt 34.663207 13793.695913
run17_high2_noise500.txt 18.720997 650.269414 (normal)
run18_high12_noise500.txt 35.275871 12591.228992
run19_low1_noise500.txt 13.781546 696.940035
run20_low2_noise500.txt 0.467614 37.075402 (normal)

Fig. 6. Derivative path anomaly score (red) for the 20 traces in Table 3. the charge-discharge cycles (triangle waveform) are too small to be seen.
A path model assigns errors to points in a time series depending on the distance to the path traced by the features of a model waveform, such as its derivatives or low pass filtered values. A path model is more constrained than a state machine model generated by rule induction and therefore able to detect anomalies that a state machine would miss. Experimentally, a path model also gives more accurate results than data compression models [2], which tend to miss transient anomalies.
A desirable property for a time series model is a parameterized description which is understandable and editable by humans. A compresion model does not have this property. A state machine model does. Our implementation of a path model does not in its current form, but it could if we approximate the model path by a piecewise linear or spline approximation. The number of vertices needed to represent the path should be similar to the model produced by GECKO in our previous work. For the TEK series, this is about 14 to 17 segments. A segment model would also speed testing because each test point would require fewer distance calculations.
We modeled only one-dimensional data (increasing it to 3 dimensions), but it would be straightforward to extend this technique to any number of dimensions, either by using more inputs, or by deriving more features of the input. It is also easy to model multiple training series.
An open source implementation of the path modeling program used to generate these results is available as tsad1.cpp (for derivative modeling) and tsad3.cpp (for filter modeling). See comments for usage.
[1] S. Salvador, P. Chan, J. Brodie, Learning States and Rules for Time Series Anomaly Detection, Florida Tech TR-CS-2003-05, 2003.
[2] M. Mahoney, Instantaneous Compression for Anomaly Detection in NASA Value Solenoid Current Traces, 2003.
Feb. 15, 2004 - version 1, results for derivative modeling only.
Feb. 23, 2004 - added results for filter path modeling.