By Matt Mahoney
Florida Institute of Technology
The purpose of this dissertation is to estimate the cost of natural language modeling, an unsolved problem which is central to artificial intelligence (AI). Knowing the difficulty of the problem, without actually solving it, would allow one to make an intelligent decision as to whether an AI project is worth pursuing, and if so, how much effort should be invested.
By cost, I mean the information content (in bits) of the language model for a natural language such as English. The complexity of the model is the dominant factor in determining its cost in dollars. A model is an algorithm that estimates the probability, P(x), of observing any given text string x in human communication. Having a good model is critical to AI applications such as speech recognition, optical character or handwriting recognition, language translation, or natural language interfaces to databases or search engines. The problem is unsolved, in that no model performs as well as humans, either directly (by estimating P(x)), or in any AI application. This is in spite of enormous effort since Alan Turing first proposed the idea of artificial intelligence in 1950.
Turing estimated that it would take 109 bits of memory to solve the AI problem, but offered no explanation for this figure. My approach is to find an empirical relationship between the size of a model (the amount of memory it requires) and its performance (how well it estimates P(x)), and compare with human performance. I did this for over 30 published statistical language models, obtaining the following.

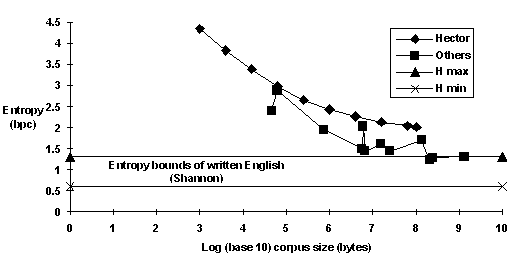
Fig. 1. Comparison of model size vs. performance.
The performance of the model is measured as the entropy in bits per character (bpc), where lower numbers are better. If we take a random string x from a large corpus of text, then a good language model is likely to assign a higher value to P(x) than a poor one. For instance, a good model would assign P(roses are red) > P(roses red are), and since the former would be more likely to appear as a test string, a higher probability usually indicates a better model. If x is very long (megabytes), then this test is very accurate because it effectively combines many smaller tests.
The entropy measure, defined as H = 1/|x| log2 1/P(x), is independent of the length of the test string, |x|, and decreases as P(x) goes up. It is identical to the best compression ratio that can be obtained with an optimal encoding of x. Indeed, many of the test points in fig. 1 are data compression programs.
The size of a statistical language model depends on the amount of training text used to train the model. The minimum amount of memory needed is simply the memory needed to store the training data. This can be reduced somewhat by compressing the data, using the model itself to do the compression. Thus, a model trained on 108 characters that compresses to 2 bpc needs at least 2 x 108 bits. The actual amount would be more, depending on the implementation, but we are more interested in finding the lower bound, which depends only on easily measurable quantities.
In 1950, Claude Shannon estimated that the entropy of written English is between 0.6 and 1.3 bpc, based on how well human subjects could predict the next character in a text string selected at random from a book. Thus, fig. 1. suggests that the AI problem is close to being solved, and that a solution would require about 108 to 1010 characters of training data (108 to 1010 bits after compression), in agreement with Turing.
My poster Text Compression as a Test for Artificial Intelligence (compressed PostScript, 1 page), published in the July, 1999 AAAI conference proceedings, supports my statistical modeling approach to this problem.
The dissertation proposal (compressed PostScript, 44 pages) was accepted Dec. 1, 1999.
Bibliography (HTML) of related work.
The second source of error is in Shannon's estimated entropy of English, which has never been improved upon. Cover and King (1978) removed the uncertainty in interpreting the results of Shannon's character guessing game by having subjects assign odds and bet on the next letter, but the test is tedious in practice and succumbs to the human tendency to overestimate unlikely events.
My dissertation addresses both sources of uncertainty. First, I plan to develop a language model, incrementally adding character, lexical, semantic, and syntactic constraints, to develop a smooth set of data points like the Hector data, but hopefully better. Second, I plan to refine the estimate of the entropy of the test data by using a form of the Shannon game that reduces the uncertainty in the interpretation of the results.
The character model was implemented as a neural network, in order to develop techniques that could be extended to higher level models. In Oct. 1999, I submitted Fast Text Compression with Neural Networks (HTML) to the FLAIRS special track on neural networks. The paper was accepted, and I presented it on May 23, 2000.
I have not yet implemented a lexical model, but I showed the feasibility of learning one in A note on lexical acquisition in text without spaces.
Sr r(pr - pr+1) log2 r £ H £ Sr pr log2 1/pr
Shannon obtained p1 = 0.8, p2 = 0.07, ..., and bounds of 0.6 to 1.3 bpc. The range of uncertainty could be reduced by making the pr more equal as follows.
Return to my Home Page