Check my WWW page for up to date information, you are always welcome to send me e-mail.
Lectures are from 1pm to 1:50pm Mondays, Wednesday, and Fridays in SKU, room 120. Find the zoom meetings on Canvas.
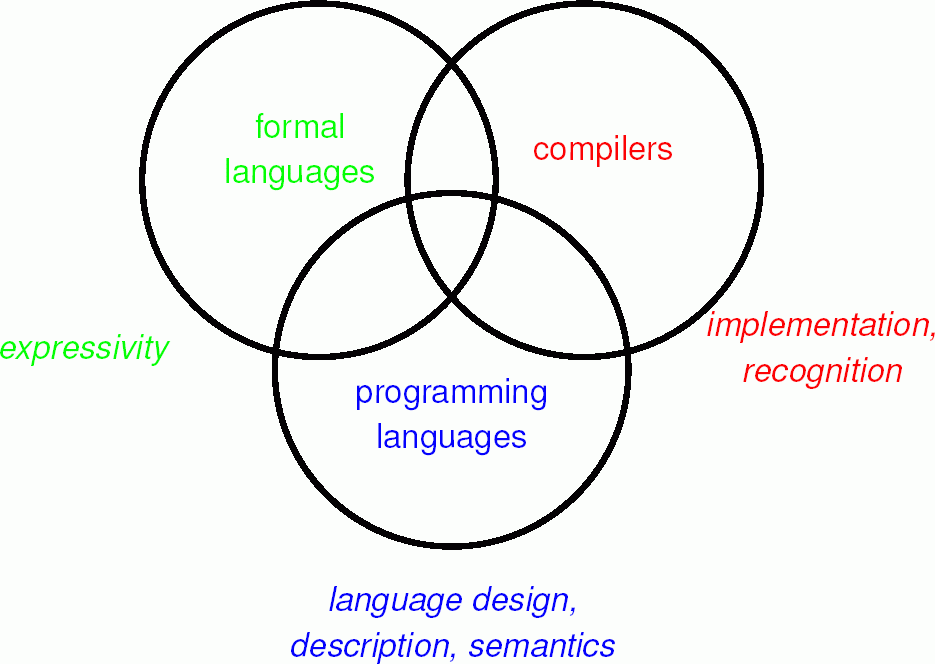
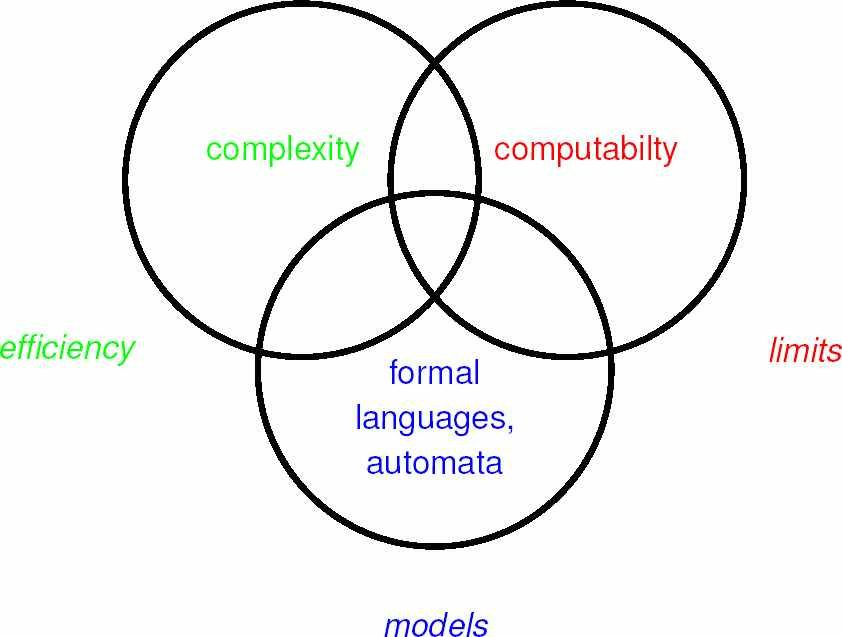
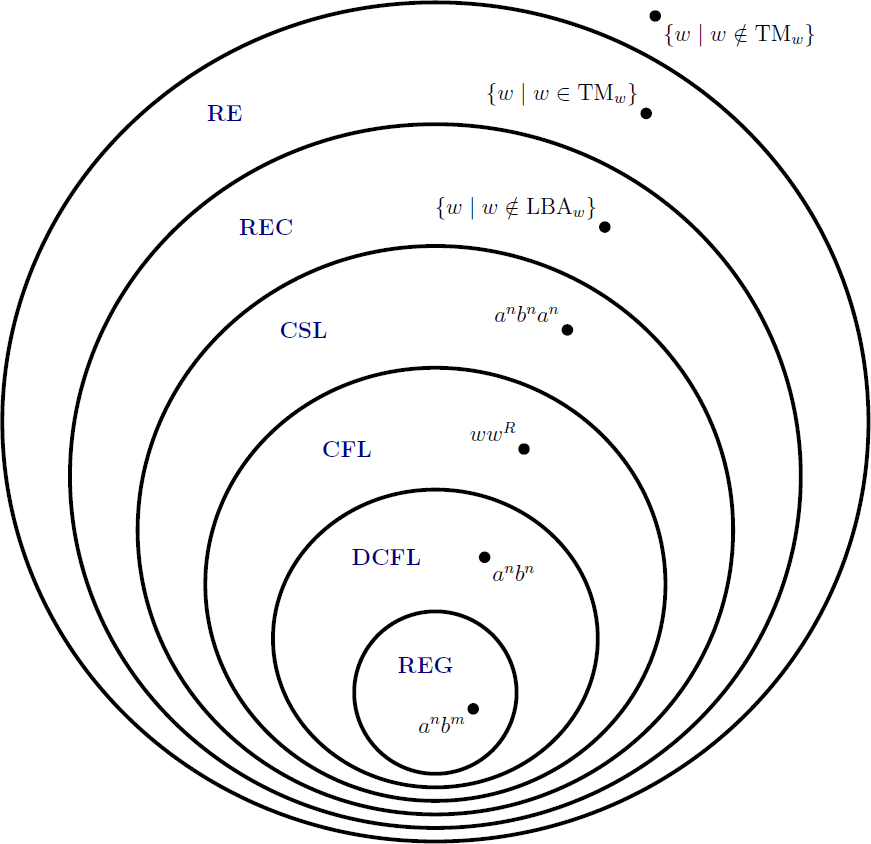
CSE 4083 Formal Languages and Automata Theory. Presents abstract models of computers (finite automata, pushdown automata and Turing machines) and the language classes they recognize or generate (regular, context-free and recursively enumerable). Also presents applications of these models to compiler design, algorithms and complexity theory. Prerequisite: CSE 2010.
Mathematical sophistication is required, in particular discrete math. There will be no programming projects.
The textbook for the class is:
| Linz |
Peter Linz and Susan Rodgers. Introduction to Formal Languages, and Automata, seventh edition. Sudbury, Massachusetts: Jones & Bartlett, 2022. ISBN-13: 978-1284231601 |
 |
| Linz |
Peter Linz. Introduction to Formal Languages, and Automata, sixth edition. Sudbury, Massachusetts: Jones & Bartlett, 2017. ISBN-13: 978-1-284077247 |
 |
Other books are similar and cover the same material. In particular the book by Hopcroft, Motwani, and Ullman (HMU) is very similar, and sometimes used as the textbook in this course.
| Hopcroft |
John E. Hopcroft, Rajeev Motwani, and Jeffrey D. Ullman. Introduction to Automata Theory, Languages, and Computation, third edition. Boston, Massachusetts: Pearson/Addison Wesley, 2007. ISBN-13: 978-0-321-45536-3 |
 |
| Kozen | Dexter Campbell Kozen. Automata Theory and Computability. New York: Springer, 1997. ISBN: 978-1-4612-7309-7. DOI 10.1007/978-1-4612-1844-9 |
 |
| Harrison | Michael A. Harrison. Introduction to Formal Language Theory. 1978. |
 |
| Sudkamp | Thomas A. Sudkamp. Languages and Machines: An introduction to the Theory of Computer Science, third edition. Boston, Massachusetts: Pearson/Addison-Wesley Education, 2006. ISBN: 9780321322210. |
 |
| Floyd |
Robert W. Floyd and Richard Beigel. The Language of Machines: An introduction to the Computability and Formal Languages, ? edition. New York: New York: Computer Science Press, 1994 ISBN: 9780716782667. |
 |
| Goddard |
Wayne Goddard. Introducing the Theory of Computation. DOI ISBN: 9780763741256. Sudbury, Massachusetts: Jones & Bartlett, 2008. |
 |
| Singh |
Arindama Singh. Elements of Computation Theory. DOI ISBN: 978-1-84882-497-3. London: Springer, 2009. |
 |
| math | automata | grammar | expressions | properties | |
|---|---|---|---|---|---|
| Introduction | 1.1 | 1.2 | |||
| Regular | 2 | 3.3 | 3.1, 3.2 | 4 | |
| Context-Free | 7 | 5, 6 | algebra | 8 | |
| Context-Sensitive | 10.5 | 11.3 | |||
| Recursive enumerable | 9, 10 | 11.2 | λ | ||
| Chapter 13: Other Models of Computation | |||||
| Chapter 14: An Overview of Complexity Theory | |||||
| math | automata | grammar | expressions | properties | |
|---|---|---|---|---|---|
| Introduction | 1 | ||||
| Regular | 2 | Ex 5.1.4 | 3 | 4 | |
| Context-Free | 6 | 5 | algebra | 7 | |
| Context-Sensitive | LBA | CSG | |||
| Recursive enumerable | 8 | λ | |||
| Chapter 10: Intractable Problems | |||||
| Chapter 11: Additional Classes of Problems | |||||
I think the ones by Busch are the best and I have provided Panopto recordings. Ullman's follows his own book, of course, and so are not focused on the way this class is organized. Linz' notes are not as extensive at Busch's. Each grid is cross-listed with Wikipedia articles which are often quite good on these topics.
The Udacity course "Computability, Complexity & Algorithms" is a somewhat different course, but some the lectures on topics common with our class are quite good. Watch the full course at Udacity.
